Sine meaning – Unveiling the essence of sine, this exploration delves into the mathematical concept, unraveling its properties, applications, and historical significance. Prepare to be captivated as we navigate the fascinating world of trigonometry and uncover the power of sine.
In the realm of mathematics, sine holds a pivotal position as a trigonometric function that measures the ratio of the opposite side to the hypotenuse in a right-angled triangle. This fundamental concept forms the cornerstone of numerous applications, from calculating angles and lengths to solving complex problems in physics and engineering.
Definition of Sine
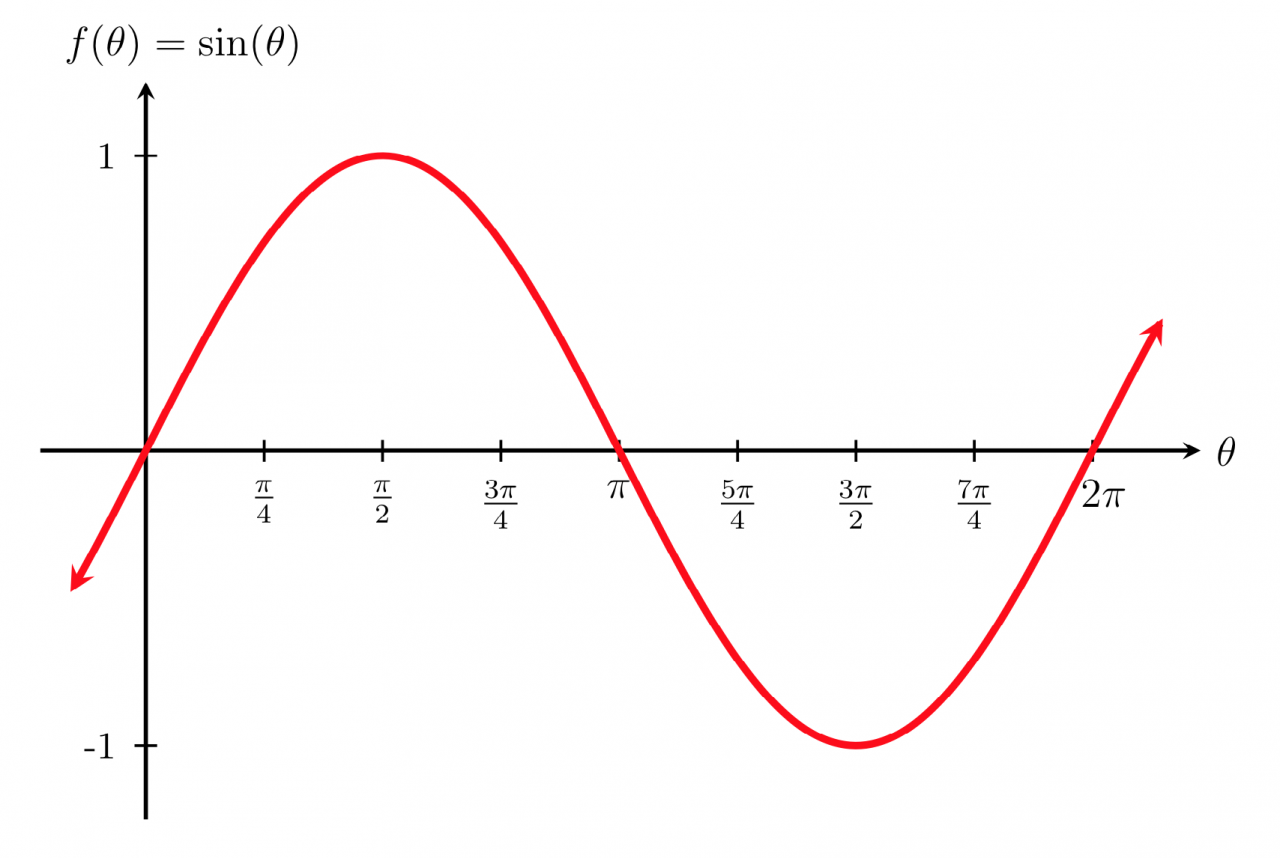
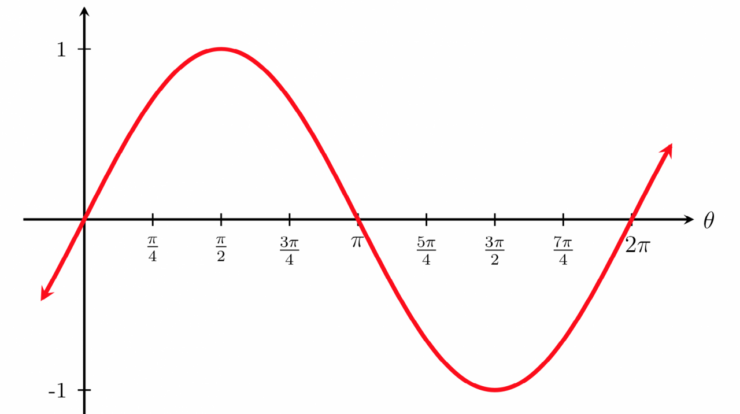
Sine is a trigonometric function that measures the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle. It is defined as the vertical coordinate of a point on the unit circle that corresponds to a given angle.
The sine of an angle θ is denoted as sin(θ) and can be calculated using the following formula:
sin(θ) = opposite/hypotenuse
Properties of Sine
Sine has several key properties that affect its behavior:
- Periodicity:Sine is a periodic function with a period of 2π. This means that it repeats itself every 2π radians.
- Amplitude:The amplitude of sine is 1, which means that it oscillates between -1 and 1.
- Range:The range of sine is [-1, 1].
Applications of Sine
Sine has a wide range of applications in various fields, including:
- Physics:Sine is used to describe the motion of objects in periodic motion, such as pendulums and springs.
- Engineering:Sine is used to analyze the forces and stresses in structures, such as bridges and buildings.
- Music:Sine is used to create the waveforms that produce musical sounds.
Historical Development of Sine: Sine Meaning
The concept of sine was first developed by ancient Greek mathematicians, including Hipparchus and Ptolemy. They used sine to calculate the angles and lengths of triangles, and to develop trigonometric tables.
In the 17th century, Isaac Newton developed the calculus, which allowed mathematicians to better understand the properties of sine and other trigonometric functions.
Today, sine is one of the most widely used trigonometric functions in mathematics, science, and engineering.
Last Recap
Through this journey, we have delved into the multifaceted nature of sine, exploring its mathematical underpinnings, practical applications, and historical evolution. Its versatility and significance continue to inspire mathematicians and scientists alike, shaping our understanding of the world around us.
FAQ Compilation
What is the definition of sine?
Sine is a trigonometric function that calculates the ratio of the opposite side to the hypotenuse in a right-angled triangle.
What are the key properties of sine?
Sine is a periodic function with an amplitude of 1 and a range of [-1, 1]. It is an odd function, meaning it is symmetrical about the origin.
What are some practical applications of sine?
Sine is used in various fields, including physics, engineering, and music, to calculate angles, lengths, and wave patterns.